quinta-feira, 4 de abril de 2024
domingo, 19 de novembro de 2017
130 - Teorema de Viviani
Vincenzo Viviani (1622-1703) foi matemático, cientista italiano, colaborador de Galileu Galilei (1564-1642) e autor da seguinte pérola da geometria plana.
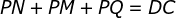
Como os leitores bem observaram, o teorema de Viviani é consequência direta de outro teorema ( que aqui chamaremos de lema V ) que diz que ( veja diagrama a seguir ) se temos um triângulo isósceles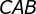 e
e 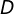 é um ponto que se encontra entre os vértices da base, então as distâncias
é um ponto que se encontra entre os vértices da base, então as distâncias 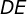 e
e 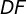 deste ponto às laterais do triângulo são tais que
deste ponto às laterais do triângulo são tais que 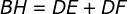 , sendo que
, sendo que 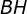 é a altura relativa à lateral
é a altura relativa à lateral 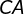 .
.
Este resultado, combinado com o fato de que as três alturas de um triângulo equilátero ( que também é isósceles ) são congruentes, nos diz que, se o triângulo  é equilátero , se
é equilátero , se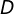 é um ponto do interior do mesmo, se
é um ponto do interior do mesmo, se 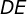 ,
, 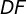 e
e 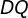 são as distâncias deste ponto aos lados do triângulo, então
são as distâncias deste ponto aos lados do triângulo, então 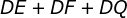 é igual a qualquer uma das três alturas do triângulo equilátero
é igual a qualquer uma das três alturas do triângulo equilátero  . A seguir, a demonstração do lema V , por semelhança de triângulos.
. A seguir, a demonstração do lema V , por semelhança de triângulos.
Se o triângulo 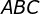 é equilátero e
é equilátero e 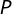 é um ponto interior, então a soma das distâncias de
é um ponto interior, então a soma das distâncias de 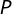 aos lados do triângulo é igual à altura do mesmo, ou seja,
aos lados do triângulo é igual à altura do mesmo, ou seja,
Neste artigo daremos quatro demonstrações . A primeira delas é a mais comum encontrada na rede por ser mais direta e econômica. No entanto, é interessante verificar as estratégias geométricas utilizadas na demonstração do teorema de Viviani sem o uso do conceito de área. A segunda e a quarta demonstração é de Marcus Bronzi e de Luis Renato, respectivamente, professores da UFU. A terceira é deste administrador, aluno da mesma Instituição.
Seja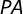 ,
, 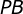 e
e 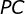 os segmentos que unem o ponto
os segmentos que unem o ponto 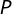 aos vértices
aos vértices  do triângulo, respectivamente. A área do triângulo
do triângulo, respectivamente. A área do triângulo 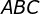 é a soma da áreas dos triângulos
é a soma da áreas dos triângulos 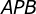 ,
, 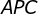 e
e 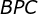 . Portanto,
. Portanto,
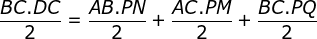
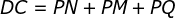
Primeira demonstração
Seja
Mas como o triângulo 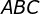 é equilátero, temos
é equilátero, temos 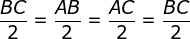 e cancelando estes fatores na expressão, chegamos à
e cancelando estes fatores na expressão, chegamos à
Segunda demonstração
1) Trace o segmento 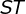 paralelo a base
paralelo a base  , passando por
, passando por 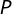 e limitado pelos lados do triângulo;
e limitado pelos lados do triângulo;
2) Pelo teorema das paralelas, concluímos que o triângulo 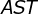 também é equilátero;
também é equilátero;
3) Trace a reta 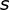 paralela à
paralela à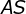 e passando por
e passando por 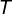 ;
;
4) Como 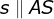 e
e 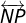 é perpendicular à
é perpendicular à 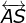 , então
, então 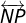 é perpendicular à
é perpendicular à 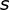 ;
;
5) Seja 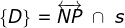 ;
;
6) Como o triângulo 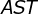 é equilátero, temos
é equilátero, temos  ;
;
7) Nos triângulos retângulos 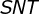 e
e 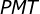 obtemos, pela soma dos ângulos internos, que
obtemos, pela soma dos ângulos internos, que  ;
;
8)  , por ser oposto à
, por ser oposto à  pelo vértice;
pelo vértice;
9) Usando soma dos ângulos internos no triângulo 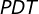 obtemos
obtemos  ;
;
10) Pelo caso ALA ( ângulo, lado, ângulo ) de congruência, obtemos 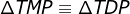 , logo
, logo 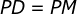 ;
;
11) A altura 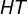 do triângulo
do triângulo 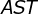 relativa ao lado
relativa ao lado 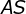 tem a mesma medida que
tem a mesma medida que 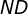 , pois
, pois 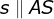 . Desta forma,
. Desta forma, 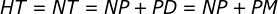 ;
;
12) Por fim, como o triângulo 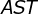 é equilátero, a altura relativa ao lado
é equilátero, a altura relativa ao lado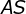 tem a mesma medida que a altura relativa ao lado
tem a mesma medida que a altura relativa ao lado 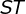 , de forma que a altura do triângulo equilátero maior
, de forma que a altura do triângulo equilátero maior 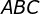 é
é 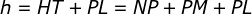 .
.
Terceira demonstração
1) Trace o segmento 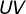 , paralelo a base
, paralelo a base  , passando por
, passando por 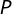 e limitado pelos lados do triângulo;
e limitado pelos lados do triângulo;
2) Pelo teorema das paralelas, concluímos que o triângulo 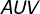 também é equilátero;
também é equilátero;
3) Trace o segmento 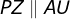 com
com 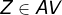 ,
, 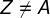 e
e 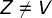 ;
;
4) Pelo teorema das paralelas, concluímos que o triângulo 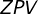 é equilátero e possui as três alturas congruentes, logo
é equilátero e possui as três alturas congruentes, logo 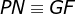 ;
;
5) Trace o segmento 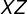 , paralelo a base
, paralelo a base  e limitado pelos lados do triângulo nos pontos
e limitado pelos lados do triângulo nos pontos 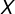 e
e 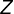 ;
;
6) Pelo teorema das paralelas, concluímos que o triângulo 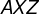 é equilátero;
é equilátero;
7) Trace o segmento 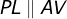 com
com  ,
, 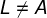 e
e 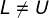 ;
;
8) Pelo teorema das paralelas, concluímos que o triângulo 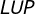 é equilátero;
é equilátero;
9) Como 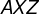 e
e 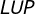 são equiláteros e ainda
são equiláteros e ainda 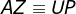 , conclui-se que
, conclui-se que 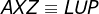 pelo critério de congruência
pelo critério de congruência 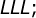
10) Logo, 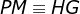 e
e 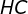 ( altura do triângulo equilátero
( altura do triângulo equilátero 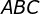 )
) 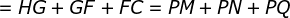 .
.
Quarta demonstração
Como os leitores bem observaram, o teorema de Viviani é consequência direta de outro teorema ( que aqui chamaremos de lema V ) que diz que ( veja diagrama a seguir ) se temos um triângulo isósceles
Artigo relacionado: 052-Generalização do Teorema de Viviani
Assinar:
Postagens (Atom)






